题目内容
5.奇函数f(x)在(-∞,0)上单调递减,若f(2)=0,则不等式f(x)<0的解集是(-2,0)∪(2,+∞).分析 根据条件判断函数的单调性,根据函数奇偶性和单调性之间的关系,作出函数f(x)的图象,利用数形结合将不等式进行转化即可解不等式即可.
解答  解:∵奇函数f(x)在(-∞,0)上单调递减,若f(2)=0
解:∵奇函数f(x)在(-∞,0)上单调递减,若f(2)=0
∴函数f(x)在(0,+∞)上单调递减,若f(-2)=-f(2)=0,
作出函数f(x)的图象如图:
则不等式f(x)<0的解集是(-2,0)∪(2,+∞),
故答案为:(-2,0)∪(2,+∞)
点评 本题主要考查不等式的解集,利用函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.如图为某几何体的三视图,则该几何体的表面积为( )


| A. | 20+2π | B. | 20+3π | C. | 24+2π | D. | 24+3π |
16.一个几何体的三视图如图所示,如果该几何体的侧面面积为12π,则该几何体的体积是( )

| A. | 4π | B. | 12π | C. | 16π | D. | 48π |
13.在直三棱柱ABC-A′B′C′中,所有的棱长都相等,M为B′C′的中点,N为A′B′的中点,则AM与BN所成角的余弦值为( )
| A. | $\frac{{2\sqrt{5}}}{7}$ | B. | $\frac{{\sqrt{35}}}{14}$ | C. | $-\frac{{2\sqrt{5}}}{7}$ | D. | $-\frac{{\sqrt{35}}}{14}$ |
20.已知函数f(x)=lnx-f′(1)x2+2x-1,则f(1)的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
10.阅读如图程序框图,为使输出的数据为15,则①处应填的数字为( )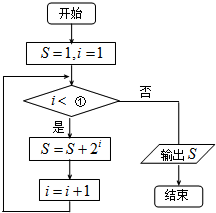

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.等比数列{an}中,a5、a7是函数f(x)=x2-4x+3的两个零点,则a3•a9等于( )
| A. | -4 | B. | -3 | C. | 4 | D. | 3 |
15.如图是一个几何体的三视图,则该几何体的体积为( )


| A. | $\frac{80}{3}$ | B. | $\frac{70}{3}$ | C. | 23 | D. | 24 |