题目内容
1.已知函数f(x)=ex-ax在(-∞,0)上是减函数,则实数a的取值范围是[1,+∞).分析 函数f(x)=ex-ax在区间(-∞,0)上是减函数?函数f′(x)=ex-a≤0在区间(-∞,0)上恒成立,
?a≥[ex]max在区间(1,+∞)上成立.
解答 解:f′(x)=ex-a,
∵函数f(x)=ex-ax在(-∞,0)上是减函数,
∴函数f′(x)=ex-a≤0在区间(-∞,0)上恒成立,
∴a≥[ex]max在区间(-∞,0)上成立.
而ex<e0,
∴a≥1.
故答案为:[1,∞).
点评 正确把问题等价转化、熟练掌握利用导数研究函数的单调性、极值与最值等是解题的关键.

练习册系列答案
相关题目
12.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增).根据此诗,可以得出塔的顶层和底层共有( )
| A. | 3盏灯 | B. | 192盏灯 | C. | 195盏灯 | D. | 200盏灯 |
16.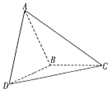 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
6.△ABC的内角A,B,C的对边分别为a,b,c,已知cosC=$\frac{1}{4}$,a=1,c=2,则△ABC的面积为( )
| A. | $\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
13.若0<a<b<1,c>1,则( )
| A. | ac>bc | B. | abc>bac | C. | logab>logba | D. | logac<logbc |
10.已知p>0,q>0,随机变量ξ的分布列如下:
若E(ξ)=$\frac{4}{9}$.则p2+q2=( )
| ξ | p | q |
| P | q | p |
| A. | $\frac{4}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | 1 |