题目内容
已知p:x2-x≥6,q:x∈Z,若“p∧q”与“?q”同时为假命题,则x的值构成的集合为 .
考点:复合命题的真假
专题:常规题型
分析:先判断组成复合命题的简单命题的真假,在根据真值表进行判断.
解答:
解∵p∧q为假命题
∴p或q至少有一个是假命题
又∵¬p为假命题
∴p为真命题
∴q一定为假命题,由此可得:x2-x<6,并且x∈Z
∴x的解集为{x|-2<x<3}并且x∈Z
∴故答案为{-1,0,1,2}
故答案为{-1,0,1,2}
∴p或q至少有一个是假命题
又∵¬p为假命题
∴p为真命题
∴q一定为假命题,由此可得:x2-x<6,并且x∈Z
∴x的解集为{x|-2<x<3}并且x∈Z
∴故答案为{-1,0,1,2}
故答案为{-1,0,1,2}
点评:进行判断的真值表:
本题主要是真假命题的判断,同时还涉及到二元一次方程的求解,一般求解有两种方法,求根公式法和因式分解法,能分解的尽量分解,解题的时候运算量更加小也更加快捷.
| p | q | p∧q | p∨q | ¬p |
| 真 | 真 | 真 | 真 | 假 |
| 真 | 假 | 假 | 真 | 假 |
| 假 | 真 | 假 | 真 | 真 |
| 假 | 假 | 假 | 假 | 真 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若角600°的终边上有一点(-3,a),则a的值是( )
A、-
| ||
B、-3
| ||
C、±
| ||
D、±3
|
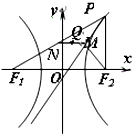 如图,已知双曲线
如图,已知双曲线