Question

3．已知函数f（x）=|x|（x-4）．
（1）用分段函数表示函数f（x），并作出y=f（x）的图象；
（2）利用图象试确定k的取值范围，使方程f（x）-k=0有一个解；有两个解；有三个解．

Answer 1

分析 （1）要根据绝对值的定义，利用零点分段法，分当x＜0时和当x≥0时两种情况，化简函数的解析式，最后可将函数y=|x|（x-4）写出分段函数的形式，根据分段函数图象分段画的原则，结合二次函数的图象和性质，可作出图象；
（2）根据（1）中函数的图象，结合函数的极大值为0，极小值为-4，可得方程|x|•（x-4）=k有一解，有两解和有三解时k的取值范围．

解答 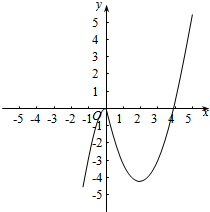解：（1）当x＜0时，y=|x|（x-4）=-x（x-4），
当x≥0时，y=|x|（x-4）=x（x-4），
综上所述：y=$\left\{\begin{array}{l}{-x（x-4），x＜0}\\{x（x-4），x≥0}\end{array}\right.$．
根据分段函数图象的作法，其函数图象如图所示；
（2）由（1）中函数的图象可得：
当k＜-4或k＞0时，方程|x|•（x-4）=k有一解，
当k=-4或k=0时，方程|x|•（x-4）=k有两解，
当-4＜k＜0时，方程|x|•（x-4）=k有三解．

点评 本题考查的知识点是分段函数的解析式及其图象的作法，函数的零点，难度不大，属于中档题．