题目内容
17.若函数y=f(x)的最小正周期是π,且图象关于点$({\frac{π}{3},0})$对称,则f(x)的解析式可以( )| A. | $y=sin({\frac{x}{2}+\frac{5π}{6}})$ | B. | $y=sin({2x-\frac{π}{6}})$ | C. | y=2sin2x-1 | D. | $y=cos({2x-\frac{π}{6}})$ |
分析 根据周期公式求解出ω,将点$({\frac{π}{3},0})$坐标带入即可得到满足要求的f(x)的解析式.
解答 解:函数y=f(x)的最小正周期是π,即T=$π=\frac{2π}{ω}$,解得:ω=2,排除A.
将点$({\frac{π}{3},0})$坐标代入,即当x=$\frac{π}{3}$时,y的值应该为0,B,C,D选项中只有D满足.
故f(x)的解析式可以是D,
故选:D.
点评 本题考虑三角函数的解析式的求法,要灵活运用函数的性质排除或者考查满足条件即可得,属于基础题.

练习册系列答案
相关题目
12.在四棱锥P-ABCD中,PA⊥底面ABCD,其中PA=2AB=2AD=2,G为三角形BCD的重心,则PG与底面ABCD所成角的正弦值为( )
| A. | $3\sqrt{2}$ | B. | $\frac{3\sqrt{11}}{11}$ | C. | $\frac{{\sqrt{19}}}{19}$ | D. | $\frac{{3\sqrt{19}}}{19}$ |
6.设有直线m,n和平面α,β,下列四个命题中,正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m?α,n?α,m∥β,l∥β,则α∥β | ||
| C. | 若α⊥β,m?α,则m⊥β | D. | 若α⊥β,m⊥β,m?α,则m∥α |
 已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.
已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.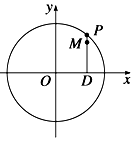 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.