题目内容
已知在四棱柱ABCD-A1B1C1D1中，侧面都是矩形，底面四边形ABCD是菱形，且AB=BC=2
，∠ABC=120°，若异面直线A1B和AD1所成的角是90°，试求AA1．
| 3 |
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：连结CD1，AC，由题意得四边形A1BCD1是平行四边形，A1B∥CD1，∠AD1C（或其补角）为A1B和AD1所成的角，由此能求出AA1．
解答：
解：连结CD1，AC，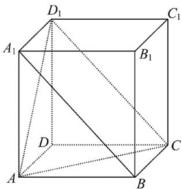
由题意得四棱柱ABCD-A1B1C1D1中，A1D1=BC，
∴四边形A1BCD1是平行四边形，
∴A1B∥CD1，
∴∠AD1C（或其补角）为A1B和AD1所成的角，
∵异面直线A1B和AD1所成的角为90°，
∴∠AD1C=90°，
∵四棱柱ABCD-A1B1C1D1中，AB=BC=2
，
∠ABC=120°，
∴AC=2
sin60°×2=6，
∴AD1=
AC=3
，
∴AA1=
=
=
．
由题意得四棱柱ABCD-A1B1C1D1中，A1D1=BC，
∴四边形A1BCD1是平行四边形，
∴A1B∥CD1，
∴∠AD1C（或其补角）为A1B和AD1所成的角，
∵异面直线A1B和AD1所成的角为90°，
∴∠AD1C=90°，
∵四棱柱ABCD-A1B1C1D1中，AB=BC=2
| 3 |
∠ABC=120°，
∴AC=2
| 3 |
∴AD1=
| ||
| 2 |
| 2 |
∴AA1=
| AD12-A1D12 |
(3
|
| 6 |
点评：本题考查四棱柱中侧棱长的求法，是中档题，解题时要注意空间能力的培养．
练习册系列答案
相关题目
下列各数中最小的数是（ ）
| A、85（9） |
| B、210（6） |
| C、1000（4） |
| D、1111111（2） |
某种商品在50个不同地区的零售价格全部介于13元与18元之间，将各地价格按如下方式分成五组：第一组[13，14）；第二组[14，15），…，第五组[17，18]．如图是按上述分组方法得到的频率分布直方图．
如图，在平面直角坐标系xOy中，点A，B，C均在单位圆上，已知点A在第一象限用横坐标是