题目内容
9.设$\overrightarrow a=({1,-2}),\overrightarrow b=({3,4}),\overrightarrow c=({2,-1}),则({\overrightarrow a+\overrightarrow b})•\overrightarrow c$=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据题意,由$\overrightarrow{a}$、$\overrightarrow{b}$的坐标计算可得向量$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,进而由向量数量积的坐标计算公式计算可得答案.
解答 解:根据题意,$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(3,4),
则$\overrightarrow{a}$+$\overrightarrow{b}$=(4,2),
又由$\overrightarrow{c}$=(2,-1),
则($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=4×2+2×(-1)=6;
故选:A.
点评 本题考查向量的数量积的计算,关键求出向量$\overrightarrow{a}$+$\overrightarrow{b}$的坐标.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.sin$\frac{π}{6}$的值等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
1.已知函数$f(x)=4{sin^2}x+4\sqrt{3}sinxcosx+5$,若不等式f(x)≤m在$[0,\frac{π}{2}]$上有解,则实数m的最小值为( )
| A. | 5 | B. | -5 | C. | 11 | D. | -11 |
17.已知$\frac{{{a^2}+2a+2}}{x}≤$$\frac{4}{{{x^2}-x}}+1$对于任意的x∈(1,+∞)恒成立,则( )
| A. | a的最小值为-3 | B. | a的最小值为-4 | C. | a的最大值为2 | D. | a的最大值为4 |
18.已知点A(0,-1)是抛物线C:x2=2py(p>0)准线上的一点,点F是抛物线C的焦点,点P在抛物线C上且满足|PF|=m|PA|,当m取最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
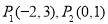 ,圆
,圆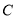 是以
是以 的中点为圆心,
的中点为圆心,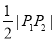 为半径的圆。
为半径的圆。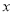 轴和
轴和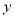 轴上截距相等,求切线方程;
轴上截距相等,求切线方程; 是圆
是圆 ,
,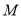 为切点,
为切点,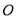 为坐标原点,且有
为坐标原点,且有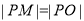 ,求使
,求使 最小的点
最小的点 的坐标.
的坐标.