题目内容
17.若实数a,b满足a>0,b>0,则“a>b”是“a+lna>b+lnb”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 据a,b的范围结合函数的单调性确定充分条件,还是必要条件即可.
解答 解:设f(x)=x+lnx,显然f(x)在(0,+∞)上单调递增,
∵a>b,
∴f(a)>f(b),
∴a+lna>b+lnb,
故充分性成立,
∵a+lna>b+lnb”,
∴f(a)>f(b),
∴a>b,
故必要性成立,
故“a>b”是“a+lna>b+lnb”的充要条件,
故选:C
点评 本题考查了函数的单调性,必要条件、充分条件与充要条件的判断,是基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.2017年某市开展了“寻找身边的好老师”活动,市六中积极行动,认真落实,通过微信关注评选“身边的好老师”,并对选出的班主任工作年限不同的五位“好老师”的班主任的工作年限和被关注数量进行了统计,得到如下数据:
(1)若”好老师”的被关注数量y与其班主任的工作年限x满足线性回归方程,试求回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并就此分析:“好老师”的班主任工作年限为15年时被关注的数量;
(2)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$).
| 班主任工作年限x(单位:年) | 4 | 6 | 8 | 10 | 12 |
| 被关注数量y(单位:百人) | 10 | 20 | 40 | 60 | 50 |
(2)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$).
12.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
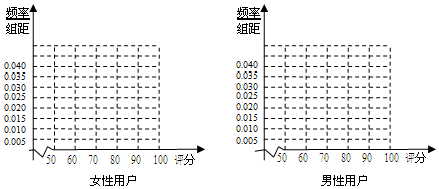
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
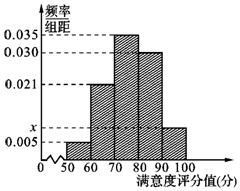 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图. 如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.
如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.