题目内容
17.已知函数f(x)=lnx-ax2在x=1处的切线与直线x-y+1=0垂直.(Ⅰ)求函数y=f(x)+xf′(x)(f′(x)为f(x)的导函数)的单调递增区间;
(Ⅱ)记函数g(x)=f(x)+$\frac{3}{2}$x2-(1+b)x,设x1,x2(x1<x2)是函数g(x)的两个极值点,若b≥$\frac{{e}^{2}+1}{e}$-1,且g(x1)-g(x2)≥k恒成立,求实数k的最大值.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的递增区间即可;
(Ⅱ)求出g(x)的导数,求出g(x1)-g(x2)的解析式,令h(x)=lnx2-$\frac{1}{2}$x2+$\frac{1}{{2x}^{2}}$,x∈(0,$\frac{1}{e}$],根据函数的单调性求出k的最大值即可.
解答 解:(Ⅰ)由题意可得:f′(x)=$\frac{1}{x}$-2ax,f′(1)=1-2a=-1,可得:a=1;
又y=f(x)+xf′(x)=lnx-3x2+1,所以y′=$\frac{1-{6x}^{2}}{x}$,(x>0),
当x∈(0,$\frac{\sqrt{6}}{6}$)时,y′>0,y单调递增;
当x∈($\frac{\sqrt{6}}{6}$,+∞)时,y′<0,y单调递减;
故函数的单调增区间为(0,$\frac{\sqrt{6}}{6}$).
(Ⅱ)g(x)=lnx+$\frac{1}{2}$x2-(1+b)x,g′(x)=$\frac{{x}^{2}-(1+b)x+1}{x}$,
因为x1,x2是g(x)的两个极值点,故x1,x2是方程x2-(1+b)x+1=0的两个根,
由韦达定理可知:$\left\{\begin{array}{l}{{x}_{1}{+x}_{2}=1+b}\\{{{x}_{1}x}_{2}=1}\end{array}\right.$;∵x1<x2,可知0<x1<1,又x1+$\frac{1}{{x}_{1}}$=1+b≥e+$\frac{1}{e}$,
令t=x+$\frac{1}{x}$,可证t(x)在(0,1)递减,由h(x1)≥h($\frac{1}{e}$),从而可证0<x1≤$\frac{1}{e}$.
所以g(x1)-g(x2)=ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{1}{2}$(x1-x2)(x1+x2)=ln${{x}_{1}}^{2}$-$\frac{1}{2}$${{x}_{1}}^{2}$+$\frac{1}{{{2x}_{1}}^{2}}$(0<x1≤$\frac{1}{e}$)
令h(x)=lnx2-$\frac{1}{2}$x2+$\frac{1}{{2x}^{2}}$,x∈(0,$\frac{1}{e}$],
h′(x)=$\frac{{-{(x}^{2}-1)}^{2}}{{x}^{3}}$≤0,所以h(x)单调减,
故h(x)min=h($\frac{1}{e}$)=$\frac{{e}^{2}}{2}$-$\frac{1}{{2e}^{2}}$-2,
所以k≤$\frac{{e}^{2}}{2}$-$\frac{1}{{2e}^{2}}$-2,即kmax=$\frac{{e}^{2}}{2}$-$\frac{1}{{2e}^{2}}$-2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,函数恒成立问题,是一道中档题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案①ab≤($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$(a,b∈R);
②若实数a>0,则lga+$\frac{1}{lga}$≥2;
③若实数a>1,则a+$\frac{4}{a-1}$≥5.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | {-1,-2} | B. | {1,2} | C. | (0,+∞) | D. | (1,2) |
| A. | 1cm | B. | 2cm | C. | 3cm | D. | $\frac{3}{2}cm$ |
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\sqrt{\frac{1+\sqrt{3}}{2}}$ |
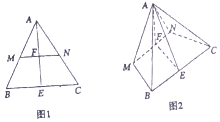 已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).
已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).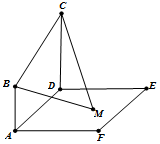 已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.
已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.