题目内容
3.已知直线l的参数方程为$\left\{\begin{array}{l}x=mt\\ y=\sqrt{3}t\end{array}\right.(t$为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2cos2θ+4ρ2sin2θ=4,直线l过曲线C的左焦点F.(1)直线l与曲线C交于A,B两点,求|AB|;
(2)设曲线C的内接矩形的周长为c,求c的最大值.
分析 (1)曲线C与直线联立,利用参数的几何意义,求|AB|;
(2)设矩形的第一象限的顶点为$({2cosθ,sinθ})({0<θ<\frac{π}{2}})$,所以$c=4({2cosθ+sinθ})=4\sqrt{5}sin({θ+φ})$,即可求c的最大值.
解答 解:(1)曲线$C:\frac{x^2}{4}+{y^2}=1$,∴$F({-\sqrt{3},0})$,曲线C与直线联立得$13{t^2}-2\sqrt{3}t-1=0$,方程两根为t1,t2,则$AB=2|{{t_1}-{t_2}}|=\frac{16}{13}$.
(2)设矩形的第一象限的顶点为$({2cosθ,sinθ})({0<θ<\frac{π}{2}})$,所以$c=4({2cosθ+sinθ})=4\sqrt{5}sin({θ+φ})$,
所以当sin(θ+φ)=1时,c最大值为$4\sqrt{5}$.
点评 本题考查三种方程的转化,考查参数方程的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.某企业为考察生产同一种产品的甲、乙两条生产线的产品合格率,同时各抽取100件产品,检验后得到如下列联表:
生产线与产品合格数列联表
请问甲、乙两线生产的产品合格率在犯错误不超过0.10的前提下是否有关?
生产线与产品合格数列联表
| 合格 | 不合格 | 总计 | |
| 甲线 | 97 | 3 | 100 |
| 乙线 | 95 | 5 | 100 |
| 总计 | 192 | 8 | 200 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
13.运行如图所示的流程图,则输出的结果S是( )
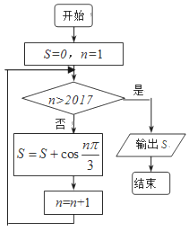

| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
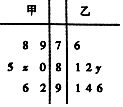 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.