题目内容
已知命题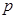 :函数
:函数 在
在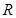 上单调递增;命题
上单调递增;命题 :不等式
:不等式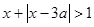 的解集为
的解集为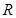 ,若
,若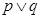 为真,
为真,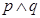 为假,求实数
为假,求实数 的取值范围.
的取值范围.
 的取值范围是
的取值范围是 .
.
解析试题分析:若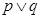 为真,则
为真,则 中至少有一个为真,
中至少有一个为真,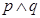 为假,则
为假,则 中至少有一个为假,由此可得
中至少有一个为假,由此可得 中一真一假,故有
中一真一假,故有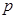 真
真 假,与
假,与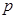 假
假 真两种情况,因此当
真两种情况,因此当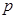 真时求出
真时求出 的取值范围,当
的取值范围,当 真时求出
真时求出 的取值范围,求出这两种情况的并集与交集,并集中除去交集部分即为所求.
的取值范围,求出这两种情况的并集与交集,并集中除去交集部分即为所求.
试题解析:若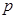 真,则
真,则 2分
2分 真
真 恒成立,设
恒成立,设 ,则
,则

 ,易知
,易知
 ,即
,即 6分
6分 为真,
为真,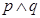 为假
为假  一真一假 7分
一真一假 7分
(1)若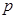 真
真 假,则
假,则 且
且 ,矛盾 9分
,矛盾 9分
(2)若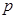 假
假 真,则
真,则 且
且 , 11分
, 11分
综上可知, 的取值范围是
的取值范围是 12分
12分
考点:简易逻辑,指数函数,绝对值不等式的解法.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 ,命题
,命题 。
。 ”为真命题,“
”为真命题,“ ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。 表示双曲线,命题
表示双曲线,命题 表示椭圆.
表示椭圆. 为真命题,求实数
为真命题,求实数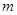 的取值范围.
的取值范围. 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个). ;命题
;命题 :不等式
:不等式 对任意
对任意 恒成立.若
恒成立.若 为真,且
为真,且 或
或 为真,求
为真,求 的取值范围.
的取值范围.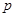 :函数
:函数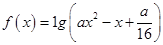 的定义域为
的定义域为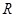 ;命题
;命题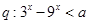 对一切的实数
对一切的实数 恒成立,如果命题“
恒成立,如果命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. ,设命题P:
,设命题P:  ;命题Q:函数f(x)=3x2+2mx+m+有两个不同的零点.求使命题“P或Q”为真命题的实数
;命题Q:函数f(x)=3x2+2mx+m+有两个不同的零点.求使命题“P或Q”为真命题的实数 的取值范围.
的取值范围. 满足
满足 (其中
(其中 ),命题q:实数
),命题q:实数
 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围; 是
是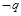 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减; 的值域是R.如果命题p或q为真命题,p且q为假命题,求
的值域是R.如果命题p或q为真命题,p且q为假命题,求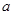 的取值范围.
的取值范围. :方程
:方程 无实数根;命题
无实数根;命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题,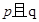 为假命题,求实数
为假命题,求实数 的取值范围。
的取值范围。