题目内容
设命题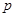 :函数
:函数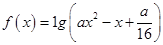 的定义域为
的定义域为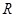 ;命题
;命题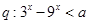 对一切的实数
对一切的实数 恒成立,如果命题“
恒成立,如果命题“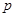 且
且 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
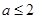
解析试题分析:对于命题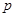 ,函数
,函数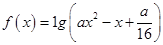 的定义域为
的定义域为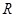 ,说明对于任意的
,说明对于任意的 ,
, 恒成立,利用一元二次不等式知识求解;对于命题q,求出
恒成立,利用一元二次不等式知识求解;对于命题q,求出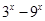 的最大值,让
的最大值,让 大于
大于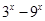 的最大值;命题“
的最大值;命题“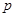 且
且 ”为假命题,说明
”为假命题,说明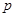 、
、 至少一假,讨论求解.
至少一假,讨论求解.
试题解析:命题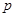 :对于任意的
:对于任意的 ,
, 恒成立,则需满足
恒成立,则需满足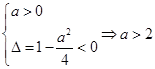 ,
, 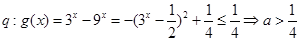 4分
4分
因为“ ”为假命题,所以
”为假命题,所以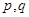 至少一假
至少一假
(1)若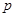 真
真 假,则
假,则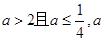 是空集。 5分
是空集。 5分
(2)若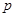 假
假 真,则
真,则 7分
7分
(3)若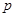 假
假 假,则
假,则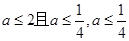 9分
9分
所以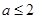 10分
10分
考点:命题及其关系、一元二次不等式恒成立问题、函数最值求法.

练习册系列答案
相关题目
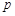 :函数
:函数 在区间
在区间 上单调递减;命题
上单调递减;命题 :函数
:函数 的最小值不大于0.如果命题
的最小值不大于0.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.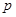 :“不等式
:“不等式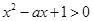 对任意
对任意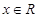 恒成立”,命题
恒成立”,命题 :“方程
:“方程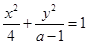 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若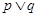 为真命题,
为真命题,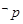 为真,求实数
为真,求实数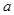 的取值范围.
的取值范围.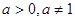 ,设
,设 :函数
:函数 在
在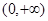 单调递减;
单调递减;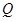 :函数
:函数 在区间
在区间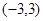 有两个零点.如果
有两个零点.如果 的取值范围.
的取值范围. :方程
:方程 无实根,命题
无实根,命题 :方程
:方程 是焦点在
是焦点在 轴上的椭圆.若
轴上的椭圆.若 与
与 同时为假命题,求
同时为假命题,求 的取值范围.
的取值范围.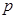 :函数
:函数 在
在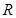 上单调递增;命题
上单调递增;命题 :不等式
:不等式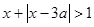 的解集为
的解集为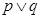 为真,
为真,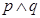 为假,求实数
为假,求实数 的取值范围.
的取值范围.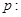 函数
函数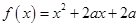 的值域为
的值域为 ,命题
,命题 方程
方程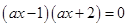 在
在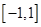 上有解,若命题“
上有解,若命题“ 或
或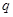 ”是假命题,求实数
”是假命题,求实数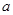 的取值范围.
的取值范围.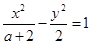 表示双曲线.
表示双曲线.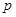 :实数
:实数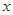 满足
满足 ,其中
,其中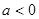 ;命题
;命题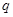 :实数
:实数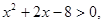 且
且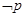 是
是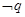 的必要不充分条件,求实数
的必要不充分条件,求实数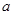 的取值范围.
的取值范围.