题目内容
设命题P:函数 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;
命题q:函数 的值域是R.如果命题p或q为真命题,p且q为假命题,求
的值域是R.如果命题p或q为真命题,p且q为假命题,求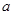 的取值范围.
的取值范围.
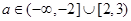
解析试题分析:由函数 在区间[-1,1]上单调递减转化为其导函数
在区间[-1,1]上单调递减转化为其导函数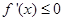 在[-1,1]上恒成立,分离变量可求解;由函数
在[-1,1]上恒成立,分离变量可求解;由函数 的值域是R转化为
的值域是R转化为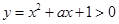 对任意的实数
对任意的实数 有意义,因此其判别式
有意义,因此其判别式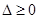 .再结合两命题的真假分类讨论求解
.再结合两命题的真假分类讨论求解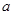 的取值范围.
的取值范围.
试题解析:p为真命题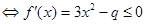 在
在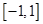 上恒成立,
上恒成立,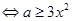 在
在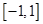 上恒成立
上恒成立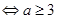 4分
4分
q为真命题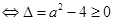 恒成立
恒成立  6分
6分
由题意p和q有且只有一个是真命题
P真q假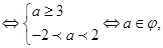 p假q真
p假q真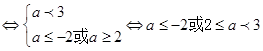
综上所述: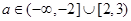 . 12分
. 12分
考点:1.命题的真值表;2.恒成立转化;3.导数判函数单调性.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线。命题
轴上的双曲线。命题 曲线
曲线 与
与 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。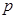 :函数
:函数 在
在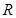 上单调递增;命题
上单调递增;命题 :不等式
:不等式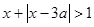 的解集为
的解集为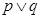 为真,
为真,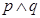 为假,求实数
为假,求实数 的取值范围.
的取值范围. 方程
方程 在[-1,1]上有解;命题
在[-1,1]上有解;命题 只有一个实数
只有一个实数 满足不等式
满足不等式 ,若命题“p∨q”是假命题,求实数
,若命题“p∨q”是假命题,求实数 的取值范围.
的取值范围.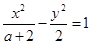 表示双曲线.
表示双曲线. :方程
:方程 无实根,命题
无实根,命题 :方程
:方程 是焦点在
是焦点在 轴上的椭圆.若
轴上的椭圆.若 与
与 同时为假命题,求
同时为假命题,求 的取值范围.
的取值范围. 若非
若非 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围.
的取值范围. 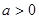 ,设命题
,设命题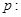 函数
函数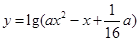 的定义域为
的定义域为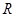 ;命题
;命题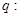 当
当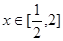 时,函数
时,函数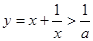 恒成立,如果
恒成立,如果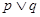 为真命题,
为真命题, 为假命题,求
为假命题,求 的取值范围.
的取值范围.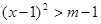 的解集为R,命题q:
的解集为R,命题q: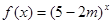 是R上的增函数,若p或q为真命题,p且q为假命题,求实数m的取值范围.
是R上的增函数,若p或q为真命题,p且q为假命题,求实数m的取值范围.