题目内容
1. 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
分析 作MH⊥BC于H,设AB=AC=m,则BM=$\frac{1}{3}$m,MH=$\frac{1}{2}$BM=$\frac{1}{6}$m,根据平行四边形的性质得OA=OC=$\frac{1}{2}AC=\frac{1}{2}m$,解直角三角形求得FC=$\frac{\sqrt{3}}{3}$m,再推导出△AOE≌△COF,证得AE=FC=$\frac{\sqrt{3}}{3}$m,进而求得OE=$\frac{1}{2}AE$=$\frac{\sqrt{3}}{6}$m,从而求得${S}_{△AOE}=\frac{\sqrt{3}}{24}{m}^{2}$,作AN⊥BC于N,根据等腰三角形的性质及解直角三角形求得BC=$\sqrt{3}m$,进而求得BF=BC-FC=$\frac{2\sqrt{3}}{3}$m,分别求出△AOE与△BMF的面积,即可得出结论.
解答 解:设AB=AC=m,则BM=$\frac{1}{3}$m,
∵O是两条对角线的交点,∴OA=OC=$\frac{1}{2}AC=\frac{1}{2}$m,
∵∠B=30°,AB=AC,
∴∠ACB=∠B=30°,
∵EF⊥AC,∴cos∠ACB=$\frac{OC}{FC}$,即cos30°=$\frac{\frac{1}{2}m}{FC}$,
∴FC=$\frac{\sqrt{3}}{3}$m,
∵AE∥FC,∴∠EAC=∠FCA,
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,∴AE=FC=$\frac{\sqrt{3}}{3}m$,
∴OE=$\frac{1}{2}AE$=$\frac{\sqrt{3}}{6}m$,
∴${S}_{△AOE}=\frac{1}{2}×OA×OE=\frac{1}{2}×\frac{1}{2}π×\frac{\sqrt{3}}{6}m$=$\frac{\sqrt{3}}{24}{m}^{2}$,
作AN⊥BC于N,∵AB=AC,
∴BN=CN=$\frac{1}{2}BC$,
∵BN=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$m,∴BC=$\sqrt{3}m$,
∴BF=BC-FC=$\sqrt{3}m-\frac{\sqrt{3}}{3}m$=$\frac{2\sqrt{3}}{3}$m,
作MH⊥BC于H,∵∠B=30°,∴MH=$\frac{1}{2}BM=\frac{1}{6}m$,
∴S△BMF=$\frac{1}{2}×BF×MH=\frac{1}{2}×\frac{2\sqrt{3}}{3}m×\frac{1}{6}m$=$\frac{\sqrt{3}}{18}{m}^{2}$,
∴$\frac{{S}_{△AOE}}{{S}_{△BMF}}$=$\frac{\frac{\sqrt{3}}{24}{m}^{2}}{\frac{\sqrt{3}}{18}{m}^{2}}$=$\frac{3}{4}$.
故答案为:3:4.
点评 本题考查两个三角形的面积的比值的求法,考查平行线性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{16}{27}$ |
| x | 1 | 2 | 3 | 4 | 5 |
| y | 220 | 250 | 285 | 340 | 405 |
回归直线的方程是:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(Ⅰ)利用最小二乘法计算年产值y(万元)关于年份代号x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(Ⅱ)预测2017年该企业的年产值.
| A. | 函数f(x)的图象关于x=-1对称 | B. | 函数f(x)的图象关于y=-1对称 | ||
| C. | 函数f(x)的图象关于(-1,0)中心对称 | D. | 函数f(x)的图象关于(-1,-1)中心对称 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 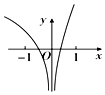 | B. |  | C. |  | D. |  |