题目内容
19.若函数f(x)=cosωx(ω>0)在$x∈[-\frac{π}{3},\frac{π}{4}]$上的最大、最小值之和为0,则ω的最小值为3.分析 ω最小时f(x)周期最大,由f(0)=1可知f(-$\frac{π}{3}$)=-1,即f(x)的半周期为$\frac{π}{3}$.
解答  解:∵f(x)在[-$\frac{π}{3}$,$\frac{π}{4}$]上最大值与最小值之和为0,f(0)=1,
解:∵f(x)在[-$\frac{π}{3}$,$\frac{π}{4}$]上最大值与最小值之和为0,f(0)=1,
∴当ω最小时,有f(-$\frac{π}{3}$)=-1.
∴$\frac{T}{2}$=$\frac{π}{3}$,于是T=$\frac{2π}{3}$.∴ω=3.
故答案为3.
点评 本题考查了余弦函数的图象与性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若方程${x^2}+\frac{y^2}{m}=4$表示焦点在x轴上的椭圆,则实数m的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (1,+∞) |
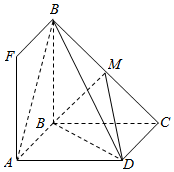 如图,正方形ABCD与正方形ABEF有一条公共边AB,且平面ABCD⊥平面ABEF,M是EC的中点,AB=2.
如图,正方形ABCD与正方形ABEF有一条公共边AB,且平面ABCD⊥平面ABEF,M是EC的中点,AB=2.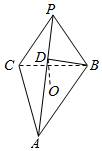 三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.