题目内容
2.已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为p2=$\frac{12}{3+si{n}^{2}θ}$,定点A(0,-$\sqrt{3}$),F1,F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2.(Ⅰ)求圆锥曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)若直线l与圆锥曲线C交于M,N两点,求|F1M|•|F1N|.
分析 (I)根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程,根据焦点坐标计算直线l的倾斜角,令F1到直线l上一点P的有向线段t为参数写出l的参数方程;,
(II)将直线l的参数方程代入曲线的直角坐标方程,得出关于t的方程,利用参数得几何意义计算|F1M|•|F1N|.
解答 解:(I)∵p2=$\frac{12}{3+si{n}^{2}θ}$,∴3ρ2+ρ2sin2θ=12.
∴曲线C的直角坐标方程为3x2+3y2+y2=12,即$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
∴F1(-1,0),F2(1,0),
∴直线AF2的斜率k${\;}_{A{F}_{2}}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$.∴直线l的倾斜角为$\frac{π}{3}$.
在l上任取一点P,设有向线段F1P的长为t,
则直线l的参数方程为$\left\{\begin{array}{l}{x=-1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数).
(II)将l的参数方程代入曲线的直角坐标方程得$\frac{(-1+\frac{1}{2}t)^{2}}{4}+\frac{(\frac{\sqrt{3}}{2}t)^{2}}{3}=1$,即5t2-4t-12=0.
设M,N对应的参数分别为t1,t2,则t1t2=-$\frac{12}{5}$.
∴|F1M|•|F1N|=|t1|•|t2|=|t1t2|=$\frac{12}{5}$.
点评 本题考查了极坐标方程,参数方程与普通方程的转化,参数方程的几何意义,属于基础题.

练习册系列答案
相关题目
17.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=1,|2$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$,则|b|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
11.若直线l:y=kx-1与曲线C:y=-$\sqrt{1-{x}^{2}}$+1有2个不同的公共点,则直线l的斜率的取值范围为( )
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (-∞,-$\sqrt{3}$) | D. | [-2,$-\sqrt{3}$)∪($\sqrt{3}$,2] |
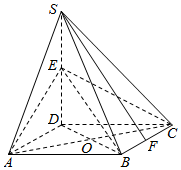 如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.
如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.