题目内容
9.下列说法正确的是( )| A. | 命题“?x0∈R,2${\;}^{{x}_{0}}$>1”的否定是“?x∈R,2x≤1” | |
| B. | 命题“若x=y,则x2=y2”的否命题是“若x=y,则x2≠y2” | |
| C. | p:?x∈R,x2+1≥1,q:在△ABC中,若sinA=$\frac{1}{2}$,则A=$\frac{π}{6}$,则p∧q为真命题 | |
| D. | 若平面α⊥平面β,直线a?α,直线b?β,则a⊥b |
分析 由特称命题的否定为全称命题,即可判断A;由否命题是既对条件否定,也对结论否定,即可判断B;
由p真,q假,运用复合命题的真值表,即可判断C;运用空间两直线的位置关系,即可判断D.
解答 解:对于A,命题“?x0∈R,2${\;}^{{x}_{0}}$>1”的否定是“?x∈R,2x≤1”,A正确;
对于B,命题“若x=y,则x2=y2”的否命题是“若x≠y,则x2≠y2”,则B不正确;
对于C,p:?x∈R,x2+1≥1,成立,p真;q:在△ABC中,若sinA=$\frac{1}{2}$,则A=$\frac{π}{6}$或$\frac{5π}{6}$,q假,
则p∧q为假命题,则C不正确;
对于D,若平面α⊥平面β,直线a?α,直线b?β,则a,b平行、相交或异面,则D不正确.
故选:A.
点评 本题考查命题的真假判断,主要是命题的否定和否命题的区别、解三角形和空间线线和面面的位置关系的判断,考查判断能力和空间想象能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知△ABC的面积为S,且$\overrightarrow{AB}$•$\overrightarrow{AC}$=S,则tan2A的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
20.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{x-y+2≥0}\\{2x+y-3≤0}\\{0≤y≤a}\end{array}}\right.$,若 z=-x+2y的最大值为3,则a的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{7}{3}$ |
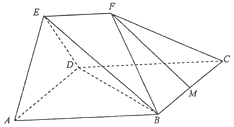 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点. - f(x),当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4。
- f(x),当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4。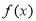 的解析式;
的解析式;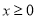 解关于
解关于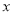 的不等式
的不等式
 ,
, ,点
,点 是线段
是线段 上的点,且
上的点,且 ,则点
,则点 的坐标是
的坐标是 B.
B. C.
C. D.
D.