题目内容
一艘船上午9：30在A处测得灯塔S在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午10：00到达B处，且与灯塔S相距8
nmile，此船的航速是32nmile/h，则灯塔S对于点B的方向角是 ．
| 2 |
考点：余弦定理的应用
专题：解三角形
分析：在△ABS中，由正弦定理可得：
=
，解出即可．
| AB |
| sinS |
| BS |
| sin∠BAS |
解答：
解：如图所示，
AB=
×32=16．
在△ABS中，由正弦定理可得：
=
，
∴
=
，
解得sinS=
．
∵0°＜S＜180°，
∴S=45°或135°．
∴∠SBy=75°或165°．
故答案为：75°或165°．
AB=
| 1 |
| 2 |
在△ABS中，由正弦定理可得：
| AB |
| sinS |
| BS |
| sin∠BAS |
∴
| 16 |
| sinS |
8
| ||
| sin30° |
解得sinS=
| ||
| 2 |
∵0°＜S＜180°，
∴S=45°或135°．
∴∠SBy=75°或165°．
故答案为：75°或165°．
点评：本题考查了正弦定理，属于基础题．
练习册系列答案
相关题目
如图，正六边形ABCDEF的中心为O，若下列命题错误的是（ ）
| A、已知数列{an}为等比数列，若m+n=p+q，m，n，p，q∈N*，则有am•an=ap•aq | ||||||||||||
B、点（
| ||||||||||||
C、若
| ||||||||||||
D、若|
|
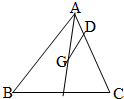
如图所示，在△ABC中，G为△ABC的重心，D在边AC上，且
=3
，则（ ）
| CD |
| DA |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知sinθ=-
，θ∈（-
，0），则cos（θ-
）的值为（ ）
| 12 |
| 13 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
（1）求值（0.064）