题目内容
已知函数f(x)=4sin2x+2sin2x-2,(0°<x<90°),当f(x)取最大值时的x=( )
| A、15° | B、22.5° |
| C、37.5° | D、67.5° |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:通过二倍角公式以及两角和的正弦函数化简函数的解析式,通过角的范围求解函数的最值,即可得到结果.
解答:
解:函数f(x)=4sin2x+2sin2x-2=2sin2x-2cos2x=2
sin(2x-45°).
0°<x<90°,2x-45°∈(-45°,135°),
当f(x)取最大值时的2x-45°=90°,
此时x=67.5°.
故选:D.
| 2 |
0°<x<90°,2x-45°∈(-45°,135°),
当f(x)取最大值时的2x-45°=90°,
此时x=67.5°.
故选:D.
点评:本题考查三角函数的最值,两角和与差的三角函数二倍角公式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2+bx+c在区间[0,+∞)上具有单调性,则实数b应满足的条件是( )
| A、b≥0 | B、b≤0 |
| C、b>0 | D、b<0 |
已知向量
、
满足|
|=
,|
-
|=
,(
,
)=
,则|
|等于( )
| a |
| b |
| a |
| 2 |
| a |
| b |
| 5 |
| a |
| b |
| π |
| 4 |
| b |
| A、2 | ||
B、
| ||
| C、3 | ||
D、2
|
为测量地面上B,C两点间的距离,在高100m的建筑物顶部选点A,在A出测得点B,C的俯角分别为30°和45°(B,C与建筑物底部在同一水平面上),且∠BAC=45°,则B,C之间的距离为( )
| A、100m | ||
B、100
| ||
C、100
| ||
| D、200m |
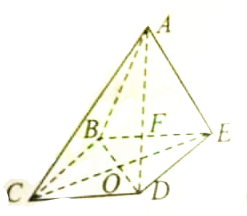 如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;
如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;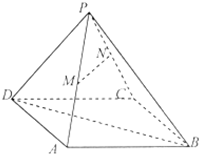 如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2
如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2