题目内容
直线y=kx是曲线y=cosx的一条切线,则实数k的取值范围为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:先设切点坐标,然后对曲线进行求导,根据导数的几何意义可得到切点的坐标,建立等式关系,求出k的表达式即可求解范围.
解答:
解:设切点为(x0,y0),而y=cosx的导数为y=-sinx,
在切点处的切线方程为y-y0=-sinx0(x-x0)
即y=-sinx0(x-x0)+cosx0=kx
即得斜率为k=-sinx0∈[-1,1].
故答案为:[-1,1].
在切点处的切线方程为y-y0=-sinx0(x-x0)
即y=-sinx0(x-x0)+cosx0=kx
即得斜率为k=-sinx0∈[-1,1].
故答案为:[-1,1].
点评:本题主要考查导数的几何意义,即函数在某点的导数值等于以该点为切点的切线的斜率,基本知识的考查.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知函数f(x)=4sin2x+2sin2x-2,(0°<x<90°),当f(x)取最大值时的x=( )
| A、15° | B、22.5° |
| C、37.5° | D、67.5° |
在△ABC中,角A、B、C所对的边分别为a,b,c,且cosA=
,则sin2
+cos2A的值为( )
| 1 |
| 3 |
| B+C |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
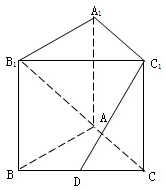 如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,已知AB=AC=AA1=2,
如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,已知AB=AC=AA1=2,