Question

3．如图，在矩形ABCD中，AD=2，AB=4，E，F分别为AB，AD的中点，现△ADE将沿DE折起，得四棱锥A-BCDE．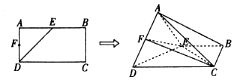

（1）求证：EF∥平面ABC；
（2）若平面ADE⊥平面BCDE，求四面体FACE的体积．

Answer 1

分析 （1）取线段AC的中点M，连结MF、MB，推导出四边形BEFM为平行四边形，从而EF∥BM，由此能证明EF∥平面ABC．
（2）推导出CE为三棱锥C-EFD的高，由此能求出四面体FACE的体积V=$\frac{1}{3}×{S}_{△EFA}×CE$．由此能求出结果．

解答 证明：（1）取线段AC的中点M，连结MF、MB，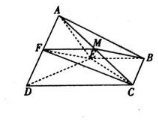
∵F是AD的中点，∴MF∥CD，且MF=$\frac{1}{2}CD$，
在折叠前，四边形ABCD为矩形，E为AB的中点，
∴BE∥CD，且BE=$\frac{1}{2}$CD，
∴MF∥BE，且MF=BE，
∴四边形BEFM为平行四边形，故EF∥BM，
又EF?平面ABC，BM?平面ABC，
∴EF∥平面ABC．
解：（2）在折叠前，四边形ABCD为矩形，AD=2，AB=4，E为AB的中点，
∴△ADE、△CBE都是等腰直角三角形，且AD=AE=EB=BC=2，
∴∠DEA=∠CEB=45°，且DE=EC=2$\sqrt{2}$，
又∠DEA+∠DEC+∠CEB=180°，∴∠DEC=90°，
又平面ADE⊥平面BCDE，平面ADE∩平面BCDE=DE，CE?平面BCDE，
∴CE⊥平面ADE，即CE为三棱锥C-EFD的高，
∵F为AD的中点，∴${S}_{△EFA}=\frac{1}{2}×\frac{1}{2}×AD×AE=\frac{1}{4}×2×2=1$，
∴四面体FACE的体积V=$\frac{1}{3}×{S}_{△EFA}×CE=\frac{1}{3}×1×2\sqrt{2}$=$\frac{2\sqrt{2}}{3}$．

点评 本题考查线面垂直的证明，考查几何体的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．