题目内容
19.已知数列{an}中,a1=1,$\frac{{a}_{n+1}}{{a}_{n}}$=1+$\frac{1}{n}$,则数列{an}的通项公式为an=n.分析 化简$\frac{{a}_{n+1}}{{a}_{n}}$=1+$\frac{1}{n}$=$\frac{n+1}{n}$,从而利用累乘法求通项公式.
解答 解:∵$\frac{{a}_{n+1}}{{a}_{n}}$=1+$\frac{1}{n}$=$\frac{n+1}{n}$,
∴$\frac{{a}_{2}}{{a}_{1}}$=$\frac{2}{1}$,
$\frac{{a}_{3}}{{a}_{2}}$=$\frac{3}{2}$,
$\frac{{a}_{4}}{{a}_{3}}$=$\frac{4}{3}$,
…,
$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n}{n-1}$;
累乘可得,
$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{4}}{{a}_{3}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{2}{1}$•$\frac{3}{2}$•$\frac{4}{3}$•…•$\frac{n}{n-1}$=n,
即an=n•a1=n,
故答案为:an=n.
点评 本题考查了数列的性质的判断与应用,同时考查了累乘法的应用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-4y2=1(a>0)的右顶点到其一条渐近线的距离等于$\frac{\sqrt{3}}{4}$,抛物线E:y2=2px的焦点与双曲线C的右焦点重合,直线l的方程为x-y+4=0,在抛物线上有一动点M到y轴的距离为d1,到直线l的距离为d2,则d1+d2的最小值为( )
| A. | $\frac{5\sqrt{2}}{2}$+2 | B. | $\frac{5\sqrt{2}}{2}$+1 | C. | $\frac{5\sqrt{2}}{2}$-2 | D. | $\frac{5\sqrt{2}}{2}$-1 |
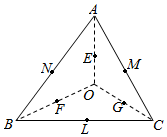 平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.