题目内容
20. 如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC.
如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC.(I)求证:PD∥平面AEF;
(Ⅱ)求几何体P-AEF的体积.
分析 (Ⅰ)在线段BC上,取BG=GF,连接PG,DG,利用中位线性质证明GD∥AF,EF∥PG,得到平面PGD∥平面AEF,从而得到PD∥平面AEF;
(Ⅱ)求出三棱锥P-AFC的体积,结合E为PC中点,可得P-AEF的体积等于三棱锥P-AFC的体积的一半得答案.
解答  (Ⅰ)证明:如图
(Ⅰ)证明:如图
在线段BC上,取BG=GF,连接PG,DG,
在△ABF中,∵BG=GF,AD=DB,∴GD∥AF,
在△PCG中,∵CF=GF,PE=EC,∴EF∥PG,
又PG∩GG,∴平面PGD∥平面AEF,
则PD∥平面AEF;
(Ⅱ)解:∵PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,
∴${V}_{P-AFC}=\frac{1}{3}{V}_{P-ABC}=\frac{1}{3}×\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{9}$,
又E为PC的中点,∴${V}_{P-AEF}=\frac{1}{2}{V}_{P-AFC}=\frac{1}{2}×\frac{4}{9}=\frac{2}{9}$.
点评 本题考查直线与平面平行的判定,在证明线面平行时,有时常采用转化为证面面平行,进一步得到线面平行,是中档题.

练习册系列答案
相关题目
10.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的实轴的两个端点为A、B,P为此双曲线上的动点,直线AP、BP的斜率均存在,分别为k1、k2.当表达式k1k2-2(ln|k1|+ln|k2|)取得最小值时,对应的双曲线的离心率为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
12.若实数a,b,c满足loga1.9<logb1.9<logc1.9,则下列关系中不可能成立的是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | a<c<b |
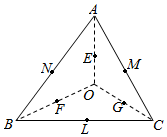 平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$. 的解集是 .
的解集是 .