题目内容
5.已知抛物线y2=4x的焦点为F,过点F的直线l与抛物线交于A、B两点.设A(x1,y1),B(x2,y2),O为原点,若$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+2(y1+y2).则直线l的方程是2x+y-2=0.分析 求得抛物线y2=4x的焦点为F(1,0),设直线l的方程为y-0=k(x-1),A(x1,y1)、B(x2,y2),把直线l的方程代入抛物线的方程,利用韦达定理求得k值后,可得直线方程.
解答 解:抛物线y2=4x的焦点为F(1,0),设直线l的方程为 y-0=k(x-1),A(x1,y1)、B(x2,y2),
把直线l的方程代入抛物线的方程可得 k2x2-(2k2+4)x+k2=0,
故有 x1•x2=1.
把直线l的方程代入抛物线的方程可得 ky2-4y-4k=0,
∴y1•y2=-4.y1+y2=$\frac{4}{k}$,
∴向量$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1•y2=x1x2+2(y1+y2)=-3,
∴k=-2,
∴直线l的方程为 y=-2(x-1),即2x+y-2=0,
故答案为:2x+y-2=0.
点评 本题主要考查抛物线的定义、标准方程,以及简单性质的应用,两个向量的数量积公式,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20. 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
10.在平面直角坐标系xOy中,点A(3,0)、B(0,3),P、Q是线段AB上的两个动点,且|PQ|=$\sqrt{2}$,则$\overrightarrow{OP}$•$\overrightarrow{OQ}$的取值范围为( )
| A. | [2,6] | B. | [4,6] | C. | [4,9) | D. | [6,9) |
15.已知函数f(x)=ax3+bx+2015,若f(2016)=4029,则f(-2016)的值为 ( )
| A. | 1 | B. | -4027 | C. | -2014 | D. | 2015 |
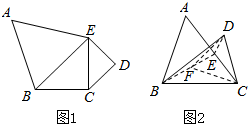 如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.
如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.