题目内容

1．设函数f（x）=2x3+3ax2+3bx+8c在x=1及x=2时取得极值．
（1）求a，b的值；
（2）求f（x）在区间[0，3]上的最值．

分析 （1）求出函数的导数，利用函数的极值点，列出方程组即可求出a，b的值；
（2）利用导函数，判断函数的单调性，然后求解极值以及端点值，即可得到函数的最值．

解答 解：（1）f′（x）=6x2+6ax+3b，
因为函数f（x）在x=1 及x=2 取得极值，
则有f′（1）=0，f′（2）=0．
即 $\left\{\begin{array}{l}{6+6a+3b=0}\\{24+12a+3b=0}\end{array}\right.$
解得a=-3，b=4．….4分
（2）由（1）可知f（x）=2x3-9x2+12x+8c，
f′（x）=6x2-18x+12=6（x-1）（x-2）．
当x∈（0，1）时，f′（x）＞0；
当x∈（1，2）时，f′（x）＜0；
当x∈（2，3）时，f′（x）＞0…6分
则当x∈[0，3]时，f（x）的最大值为f（3）=9+8c…8分
最小值为f（0）=8c，最大值为f（3）=8c…10分

点评 本题考查函数的导数的综合应用，考查转化思想以及计算能力．

练习册系列答案
相关题目
11．已知函数f（x）=ex，g（x）=$\frac{n}{2}x+m$，其中e为自然对数的底数，m，n∈R．
（1）若n=2时方程f（x）=g（x）在[-1，1]上恰有两个相异实根，求m的取值范围；
（2）若T（x）=f（x）•g（x），且m=1-$\frac{n}{2}$，求T（x）在[-1，1]上的最大值；
（3）若m=-$\frac{15}{2}$，求使f（x）＞g（x）对?x∈R都成立的最大正整数n．
12．.已知数列{an}，{bn}满足：an+bn=1，bn+1=$\frac{b_n}{{（1-{a_n}）（1+{a_n}）}}$，且a1，b1是函数f（x）=16x2-16x+3的零点（a1＜b1）．
（1）求a1，b1，b2；
（2）设cn=$\frac{1}{{{b_n}-1}}$，求证：数列{cn}是等差数列，并求bn的通项公式；
（3）设Sn=a1a2+a2a3+a3a4+…+anan+1，不等式4aSn＜bn恒成立时，求实数a的取值范围．
9．若函数f（x）=2-|x|+c有零点，则实数c的取值范围是（　　）
A．（0，1]B．[0，1]C．[-1，0）D．（0，+∞）
16．观察如图，则第（　　）行的各数之和等于20152．
A．2014B．2016C．1007D．1008
6．函数f（x）=$\frac{A}{2}$-$\frac{A}{2}$cos2（ωx+φ），（A＞0，ω＞0，0＜φ＜$\frac{π}{2}）$的图象过点（1，2），相邻两条对称轴间的距离为2，且f（x）的最大值为2．则f（1）+f（2）+…+f（2016）=2016．
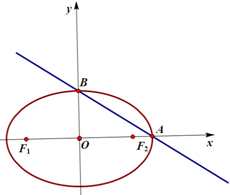13．椭圆C；$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别是F1，F2，右顶点为A，上顶点为B，坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$，椭圆的离心率是$\frac{1}{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若经过点N（0，t）的直线l与椭圆C交于不同的两点P，Q，且$\overrightarrow{PN}$=3$\overline{NQ}$，求△AON（点o为坐标系原点）周长的取值范围．
10．（1-$\frac{1}{x}$）（1+x）5的展开式中项x3的系数为（　　）
A．7B．8C．10D．5
11．一个四面体的所有棱长都等于a，则该四面体的外接球的体积等于$\frac{\sqrt{6}}{8}$πa3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网