题目内容
3.已知直角三角形的两直角边长分别为2和4,求两直角边上的中线所夹的锐角的余弦值.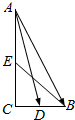
分析 作出图形,由勾股定理及重心性质求出△BGD的三边,再由余弦定理即可求得答案.
解答 解:如图所示:BC=2,AC=4,
则BD=CD=1,CE=2,AD=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
BE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
令AD,BE交于点G,则: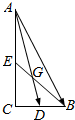
GD=$\frac{1}{3}$AD=$\frac{\sqrt{17}}{3}$,GB=$\frac{2}{3}$BE=$\frac{4}{3}\sqrt{2}$,
在△BGD中,cos∠BGD=$\frac{{GD}^{2}+{GB}^{2}-{BD}^{2}}{2GD•GB}$=$\frac{\frac{40}{9}}{\frac{136\sqrt{2}}{9}}$=$\frac{5\sqrt{2}}{34}$
点评 该题考查余弦定理及其应用,考查三角形的重心性质,属基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
11. 如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
 如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )| A. | $\sqrt{14}$ | B. | 4 | C. | $\sqrt{17}$ | D. | $\sqrt{19}$ |
13.直线kx-y=k-1与直线y=x+2-2k的交点在第二象限内,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,0) | D. | (-∞,$\frac{1}{2}$] |
 如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为15.
如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为15.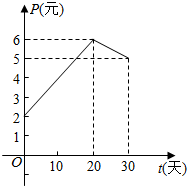 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).