题目内容
(2009•襄阳模拟)某商场举行周末有奖促销活动,凡在商场一次性购物满500元的顾客可获得一次抽奖机会.抽奖规则:自箱中一次摸出两个球,确定颜色后放回,奖金数如下表:
经测算该商场赢利为销售额的10%,已知箱中已放有2个红色球和5个蓝色球,为使本次抽奖活动不亏本,该商场应在箱中至少放入多少个其它颜色的球?(抽出任一颜色球的概率相同).
| 球的颜色 | 一红一蓝 | 两蓝 | 两红 |
| 奖金数 | 100元 | 150元 | 200元 |
分析:先确定在箱中至少放入x个其它颜色的球,获得奖金数为ξ 的取值,再求出相应的概率,从而得分布列,由期望公式即可得不等式,从而得解.
解答:解:该商场应在箱中至少放入x个其它颜色的球,获得奖金数为ξ,
则ξ=0,100,150,200
P(ξ=0)=
=
,P(ξ=100)=
=
,
P(ξ=150)=
=
P(ξ=200)=
=
,(8分)
∴Eξ=0×
+100×
+150×
+200×
=
(10分)
由已知,Eξ≤500×10%=50,即
≤50
x2+13x-66≥0 (x∈Z*)
解得:x≥4
∴该商场应在箱中至少放入4个其它颜色的球.(12分)
则ξ=0,100,150,200
P(ξ=0)=
| ||
|
| x(x-1) |
| (x+7)(x+6) |
| ||||
|
| 20 |
| (x+7)(x+6) |
P(ξ=150)=
| ||
|
| 20 |
| (x+7)(x+6) |
| ||
|
| 2 |
| (x+7)(x+6) |
∴Eξ=0×
| x(x-1) |
| (x+7)(x+6) |
| 20 |
| (x+7)(x+6) |
| 20 |
| (x+7)(x+6) |
| 2 |
| (x+7)(x+6) |
=
| 5400 |
| (x+7)(x+6) |
由已知,Eξ≤500×10%=50,即
| 5400 |
| (x+7)(x+6) |
x2+13x-66≥0 (x∈Z*)
解得:x≥4
∴该商场应在箱中至少放入4个其它颜色的球.(12分)
点评:本题以实际问题为载体,考查离散型随机变量的分布列及其期望,关键是确定变量及其取值.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
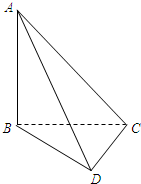 (2009•襄阳模拟)在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.
(2009•襄阳模拟)在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.