题目内容
2.设偶函数f(x)在(0,+∞)上f'(x)<0,且f(2)=0,则不等式$\frac{f(x)+f(-x)}{x}>0$的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
分析 先确定函数在(0,+∞﹚上是减函数,在(-∞,0)上是增函数,再将不等式等价变形,利用函数的单调性,即可求解不等式.
解答 解:∵偶函数f(x)在(0,+∞)上f'(x)<0,
∴函数在(0,+∞﹚上是减函数,在(-∞,0)上是增函数,
∵f(2)=0,∴f(-2)=0
不等式$\frac{f(x)+f(-x)}{x}>0$等价于$\left\{\begin{array}{l}{x>0}\\{f(x)>f(2)}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)<f(-2)}\end{array}\right.$
∴0<x<2或x<-2
故不等式$\frac{f(x)+f(-x)}{x}>0$的解集为(-∞,-2)∪(0,2),
故选D.
点评 本题考查函数单调性与奇偶性的结合,考查解不等式,考查学生的计算能力,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
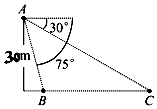 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于$60(\sqrt{3}-1)$m.