题目内容
 如图,在正方形OABC内任取一点,取到函数y=
如图,在正方形OABC内任取一点,取到函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:欲求所投的点落在阴影部分内部的概率,须结合定积分计算阴影部分平面区域的面积,再根据几何概型概率计算公式易求解.
解答:
解:根据题意,正方形OABC的面积为1×1=1,而阴影部分的面积为
dx=
x
=
,
∴正方形OABC中任取一点P,点P取自阴影部分的概率为
=
;
故选B.
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1 0 |
| 2 |
| 3 |
∴正方形OABC中任取一点P,点P取自阴影部分的概率为
| ||
| 1 |
| 2 |
| 3 |
故选B.
点评:本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,图中有5组数据,去掉( )组数据后(填字母代号),剩下的4组数据的线性相关性最大.
如图所示,图中有5组数据,去掉( )组数据后(填字母代号),剩下的4组数据的线性相关性最大.| A、A | B、C | C、D | D、E |
已知复数z=-2i,则
的虚部为( )
| 1 |
| z+1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是( )
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y-1=0 |
| D、x-y+1=0 |
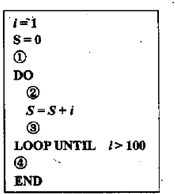 如图的语句是求S=1+2+3+…+100的一个程序,语句i=i+1应当在这个程序中的①②③④四处的哪一处才能实现上述功能( )
如图的语句是求S=1+2+3+…+100的一个程序,语句i=i+1应当在这个程序中的①②③④四处的哪一处才能实现上述功能( )