题目内容
16.已知函数f(x)(sinx+cosx)2+2cos2x-2(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[$\frac{π}{4}$,$\frac{3π}{4}$]时,求函数f(x)的值域.
分析 (1)利用二倍角和辅助角公式化简为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期;
(2)根据三角函数的性质即可得f(x)的最大值,以及取得最大值时x取值集合;
(3)当x∈[$\frac{π}{4}$,$\frac{3π}{4}$]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值,即得到f(x)的值域.
解答 解:函数f(x)=(sinx+cosx)2+2cos2x-2
化简可得:f(x)=1+2sinxcosx+1+cos2x-2=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)
(1)函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
(2)令2x+$\frac{π}{4}$=$\frac{π}{2}+2kπ$,k∈Z,
得:x=$kπ+\frac{π}{8}$.
∴当x=$kπ+\frac{π}{8}$时,f(x)取得最大值为$\sqrt{2}$.
∴取得最大值时x取值集合为{x|x=$kπ+\frac{π}{8}$,k∈Z}.
(3)当x∈[$\frac{π}{4}$,$\frac{3π}{4}$]时,
可得:2x+$\frac{π}{4}$∈[$\frac{3π}{4}$,$\frac{7π}{4}$],
∴-1≤sin(2x+$\frac{π}{4}$)≤$\frac{\sqrt{2}}{2}$
∴$-\sqrt{2}$≤$\sqrt{2}$sin(2x+$\frac{π}{4}$)≤1.
故得当x∈[$\frac{π}{4}$,$\frac{3π}{4}$]时,函数f(x)的值域为[$-\sqrt{2}$,1].
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案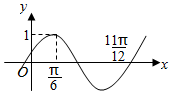 函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |