题目内容
11.已知函数f(x)=2sinxcos(x+$\frac{π}{3}$)+$\sqrt{3}$cos2x+$\frac{1}{2}$sin2x.(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间.
分析 (1)由三角函数公式化简可得f(x)=2si$n(2x+\frac{π}{3})$,由周期公式可得;
(2)解2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得f(x)的单调递增区间.
解答 解:(1)由三角函数公式化简可得:
f(x)=2sinxco$s(x+\frac{π}{3})$+$\sqrt{3}cos$2x+$\frac{1}{2}sin$2x
=2sin$x(cosxcos\frac{π}{3}-sinxsin\frac{π}{3})$+$\sqrt{3}cos$2x+$\frac{1}{2}sin$2x
=sinxcosx-$\sqrt{3}sin$2x+$\sqrt{3}cos$2x+$\frac{1}{2}sin$2x
=sin2x+$\sqrt{3}cos$ 2x=2si$n(2x+\frac{π}{3})$,
∴f(x)的最小正周期为T=$\frac{2π}{2}$=π;
(2)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,
∴解得x∈$[kπ-\frac{5π}{12},kπ+\frac{π}{12}]$(k∈Z),
∴f(x)的单调递增区间为$[kπ-\frac{5π}{12},kπ+\frac{π}{12}]$(k∈Z).
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和单调性,属基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
7.设实数x,y满足$\left\{\begin{array}{l}{2x-y+1≤0}\\{y≤-x-k}\\{x≥0}\end{array}\right.$(k为常数),若目标函数z=3x-y的最大值为-$\frac{1}{3}$,则点(x,y)构成的平面区域Ω的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
19.如图所示,在正方体ABC-A1B1C1D1中,异面直线A1D与AB1所成角( )
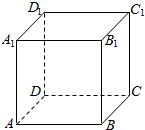

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.执行如图所示的程序框图后,输出的结果为( )
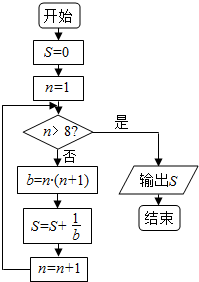

| A. | $\frac{7}{8}$ | B. | $\frac{9}{10}$ | C. | $\frac{8}{9}$ | D. | $\frac{10}{11}$ |
1.已知集合A={x|2x+a>0}(a∈R),且1∉A,2∈A,则( )
| A. | a>-4 | B. | a≤-2 | C. | -4<a<-2 | D. | -4<a≤-2 |