题目内容
设i是虚数单位，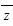
是复数z的共轭复数，若z·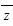i＋2＝2z，则z＝( )
A．1＋i B．1－i
C．－1＋i D．－1－i
A
[解析] 设z＝a＋bi(a，b∈R)，
则由z·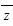i＋2＝2z得(a＋bi)(a－bi)i＋2＝2(a＋bi)，
即(a2＋b2)i＋2＝2a＋2bi，
所以2a＝2，a2＋b2＝2b，
所以a＝1，b＝1，即z＝a＋bi＝1＋i.
练习册系列答案
相关题目
题目内容
设i是虚数单位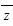，是复数z的共轭复数，若z·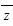i＋2＝2z，则z＝( )
A．1＋i B．1－i
C．－1＋i D．－1－i
A
[解析] 设z＝a＋bi(a，b∈R)，
则由z·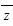i＋2＝2z得(a＋bi)(a－bi)i＋2＝2(a＋bi)，
即(a2＋b2)i＋2＝2a＋2bi，
所以2a＝2，a2＋b2＝2b，
所以a＝1，b＝1，即z＝a＋bi＝1＋i.
，构造数列{an}，使得an＝
，
B.
D.
是实数，则实数a等于( )
D．－
(i为虚数单位)，则a＋b的值为________．
＝－
＋
i，则a＝( )
