题目内容
已知a，b，c∈(0,1)，求证：(1－a)b，(1－b)c，(1－c)a不可能都大于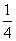
.
证明 假设三个式子同时大于，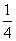
即(1－a)b>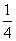，(1－b)c>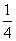，(1－c)a>，
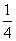三式相乘得(1－a)a·(1－b)b·(1－c)c>
，①
又因为0<a<1，所以0<a(1－a)≤(
)2＝.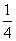
同理0<b(1－b)≤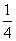，0<c(1－c)≤，
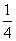所以(1－a)a·(1－b)b·(1－c)c
≤②
①与②矛盾，所以假设不成立，故原命题成立．
练习册系列答案
相关题目
表示的平面区域为D，若指数函数y=
的图像上存在区域D上的点，则a 的取值范围是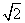 
，|β|>2
的命题是________．
题“若a2＋b2＝0，则a，b全为0(a、b为实数)”，其反设为
正确的是________．
＝
·
，写出图(2)中类似的体积关系，并证明你的结论．
<
1的________条件．