题目内容
15.在△ABC中,a,b,c分别为内角的对边,若a=$\sqrt{3}$,A=$\frac{π}{3}$,b=$\sqrt{2}$,则B=( )| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
分析 由已知利用正弦定理,特殊角的三角函数值即可求解.
解答 解:∵a=$\sqrt{3}$,A=$\frac{π}{3}$,b=$\sqrt{2}$,
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,
∵B∈(0,π),a>b,∴A>B,
∴B=$\frac{π}{4}$.
故选:A.
点评 本题主要考查了正弦定理,特殊角的三角函数值的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.复数$\frac{2}{1-i}$-2i(i为虚数单位)的共轭复数的虚部等于( )
| A. | -1 | B. | 1-i | C. | i | D. | 1 |
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,则下列结论中正确的个数是( )
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,则下列结论中正确的个数是( )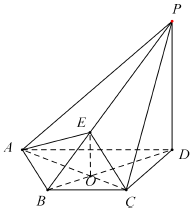 如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.
如图,在四棱锥P-ABCD中,PD⊥平面 ABCD,AC⊥BD于点O,E为线段PB 上的点,且BD⊥AE.