题目内容
5.不等式2sin2x≤1(x∈[0,2π])的解集为[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,$\frac{5π}{4}$]∪[$\frac{7π}{4}$,2π].分析 根据已知可得-$\frac{\sqrt{2}}{2}$≤sinx≤$\frac{\sqrt{2}}{2}$,根据正弦型函数的图象和性质,结合x∈[0,2π],可得答案.
解答 解:若2sin2x≤1,
则sin2x≤$\frac{1}{2}$,
则-$\frac{\sqrt{2}}{2}$≤sinx≤$\frac{\sqrt{2}}{2}$,
又∵x∈[0,2π],
∴x∈[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,$\frac{5π}{4}$]∪[$\frac{7π}{4}$,2π],
故答案为:[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,$\frac{5π}{4}$]∪[$\frac{7π}{4}$,2π].
点评 本题考查的知识点是三角不等式的解法,熟练掌握三角函数的图象和性质,是解答的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.若x,y满足约束条件$\left\{\begin{array}{l}x+y≤0\\ x-y+1≥0\\ y≥0\end{array}\right.$,则z=-2x+y的最大值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
16.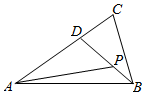 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )
 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )| A. | λ=$\frac{2}{3}$ | B. | λ=$\frac{1}{3}$ | C. | μ=$\frac{4}{9}$ | D. | μ=$\frac{1}{3}$ |
20.已知抛物线C1:x2=2py(p>0)的准线与抛物线C2:x2=-2py(p>0)交于A,B两点,C1的焦点为F,若△FAB的面积等于1,则C1的方程是( )
| A. | x2=2y | B. | x2=$\sqrt{2}$y | C. | x2=y | D. | x2=$\frac{\sqrt{2}}{2}y$ |