题目内容
【题目】已知数列{an}的前n项和是Sn,且Sn![]() =1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=
=1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() ,而b2,b5,ba14成等比数列.
,而b2,b5,ba14成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(I)Sn![]() =1(n∈N),n≥2时,Sn﹣1+
=1(n∈N),n≥2时,Sn﹣1+![]() an﹣1=1,相减可得:an
an﹣1=1,相减可得:an![]() ﹣
﹣![]() an﹣1=0,化为:an=
an﹣1=0,化为:an=![]() an﹣1.利用等比数列的通项公式可得an.数列{bn}是公差d不等于0的等差数列,且满足:b1=
an﹣1.利用等比数列的通项公式可得an.数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() =1.由b2,b5,b14成等比数列.可得
=1.由b2,b5,b14成等比数列.可得![]() =b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)设cn=anbn=
=b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)设cn=anbn=![]() ,利用错位相减法即可得出.
,利用错位相减法即可得出.
详解:
(1)Sn![]() =1(n∈N),n≥2时,Sn﹣1+
=1(n∈N),n≥2时,Sn﹣1+![]() an﹣1=1,相减可得:an
an﹣1=1,相减可得:an![]() ﹣
﹣![]() an﹣1=0,化为:an=
an﹣1=0,化为:an=![]() an﹣1.
an﹣1.
n=1时,a1+![]() =1,解得a1=
=1,解得a1=![]() .
.
∴数列{an}是等比数列,首项为![]() ,公比为
,公比为![]() .∴an=
.∴an=![]() =2×
=2×![]() .
.
数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() =1.
=1.
∵b2,b5,b14成等比数列.∴![]() =b2b14,
=b2b14,
∴(1+4d)2=(1+d)(1+13d),d≠0.解得d=2.∴bn=1+2(n﹣1)=2n﹣1.
(2)设cn=anbn=![]() .
.
求数列{cn}的前n项和Tn=![]() +……+
+……+![]() .
.
![]() =
=![]() +……+
+……+![]() +
+![]() ,
,
相减可得:![]() Tn=
Tn=![]() +4
+4![]() ﹣
﹣![]() =
=![]() +4×
+4×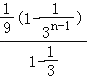 ﹣
﹣![]() ,
,
化为:Tn=2﹣![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目