题目内容
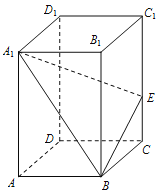
【题目】如图，已知长方体ABCD－A1B1C1D1中，AB＝3，BC＝2，CC1＝5，E是棱CC1上不同于端点的点，且
．
（1） 当∠BEA1为钝角时，求实数λ的取值范围；
（2） 若λ＝
，记二面角B1－A1B－E的的大小为θ，求|cosθ|．
【答案】（1）(
，
)．（2）
．
【解析】
试题解析：
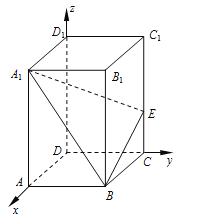
解：（1）以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立如图所示的空间直角坐标系．
由题设，知B(2，3，0)，A1(2，0，5)，C(0，3，0)，C1(0，3，5)．
因为
，所以E(0，3，5λ)．
从而
＝(2，0，－5λ)，
＝(2，－3，5－5λ)． 2分
当∠BEA1为钝角时，cos∠BEA1＜0，
所以
＜0，即2×2－5λ(5－5λ)＜0，
解得＜λ＜．
即实数λ的取值范围是(，)． 5分
（2）当λ＝
时，＝(2，0，－2)，＝(2，－3，3)．
设平面BEA1的一个法向量为n1＝(x，y，z)，
由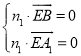
得
取x＝1，得y＝
，z＝1，
所以平面BEA1的一个法向量为n1＝(1，，1)． 7分
易知，平面BA1B1的一个法向量为n2＝(1，0，0)．
因为cos< n1，n2>＝
，
从而|cosθ|＝
． 10分
练习册系列答案
名校课堂系列答案
相关题目
