题目内容
10.已知函数f(x)=cos(2x-$\frac{π}{3}$)+2cos2x,将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )| A. | (-$\frac{π}{2}$,1) | B. | (-$\frac{π}{12}$,1) | C. | ($\frac{π}{6}$,1) | D. | ($\frac{π}{4}$,0) |
分析 由条件利用三角函数恒等变换的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得所得函数图象的一个对称中心.
解答 解:∵f(x)=cos(2x-$\frac{π}{3}$)+2cos2x=$\frac{3}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x+1=$\sqrt{3}$sin(2x+$\frac{π}{3}$)+1,
∴将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象,可得:g(x)=$\sqrt{3}$sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]+1=$\sqrt{3}$sin2x+1,
∴令2x=kπ,k∈z,可得x=$\frac{kπ}{2}$,k∈z,
∴当k=-1时,可得函数的图象的对称中心为(-$\frac{π}{2}$,1),
故选:A.
点评 本题主要考查三角函数恒等变换的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
20.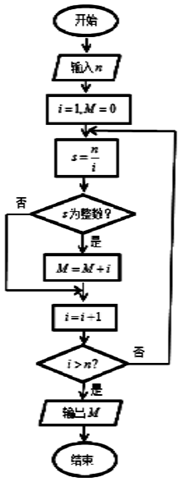 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |
5.已知z是复数,且$\frac{z+2}{i}$=1+i,则z在复平面内对应的点的坐标为( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,-3) | D. | (-1,-3) |
19.在△ABC中,a,b,c分别是角A,B,C所对的边,且$a=2,b=\sqrt{2},A=\frac{π}{4}$,则角B=( )
| A. | $\frac{5π}{6}$或 $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
 如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.
如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.