题目内容
18.已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a2+a3=8,则数列{an}的前n项和Sn=n2.分析 利用等差数列通项公式和等比数列性质列出方程组,求出a1=1,d=2,由此能求出数列{an}的前n项和Sn.
解答 解:∵等差数列{an}的公差d≠0,
且a1,a3,a13成等比数列,a2+a3=8,
∴$\left\{\begin{array}{l}{({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+12d)}\\{{a}_{1}+d+{a}_{1}+2d=8}\end{array}\right.$,
解得a1=1,d=2,
∴数列{an}的前n项和Sn=$n+\frac{n(n-1)}{2}×2={n}^{2}$.
故答案为:n2.
点评 本题考查等差数列的前n项和的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
13.“sinα=$\frac{1}{2}$“是“α=30°”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.已知函数f(x)=cos(2x-$\frac{π}{3}$)+2cos2x,将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
| A. | (-$\frac{π}{2}$,1) | B. | (-$\frac{π}{12}$,1) | C. | ($\frac{π}{6}$,1) | D. | ($\frac{π}{4}$,0) |
7.执行如图所示程序框图,若使输出的结果不大于100,则输入的整数k的最大值为( )

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为4.
如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为4.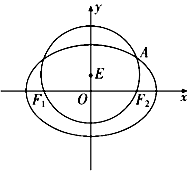 如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.