题目内容
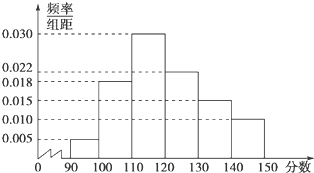
某校1000名学生的数学测试成绩分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为175人,则a的估计值是 .

考点:频率分布直方图
专题:概率与统计
分析:根据频率分布直方图,求出分数在140~150和130~140的人数是多少,即可得出正确的结论.
解答:
解:根据频率分布直方图,得;
分数在140~150的人数是1000×0.010×10=100,
分数在130~140的人数是1000×0.015×10=150,
∴分数在135~150的人数是150÷2+100=175;
∴当优秀的人数为175人时,a的估计值是135.
故答案为:135.
分数在140~150的人数是1000×0.010×10=100,
分数在130~140的人数是1000×0.015×10=150,
∴分数在135~150的人数是150÷2+100=175;
∴当优秀的人数为175人时,a的估计值是135.
故答案为:135.
点评:本题考查了频率分布直方图的应用问题,解题时应根据频率=
的关系进行解答,是基础题.
| 频数 |
| 样本容量 |

练习册系列答案
相关题目
已知实数x,y满足
,则当x+y=3时,目标函数z=
的取值范围是( )
|
| y |
| x |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
设
、
、
是单位向量,若
+
=
,则
•
的值为( )
| a |
| b |
| c |
| a |
| b |
| 2 |
| c |
| a |
| c |
A、
| ||||
B、-
| ||||
| C、1 | ||||
| D、-1 |