题目内容
已知函数f（x）=x2+2x-2，x∈（-3，1]，则f（x）的值域为 ．
考点：函数的值域
专题：函数的性质及应用
分析：配方可得二次函数的单调性，代值计算可得最值，可得值域．
解答：
解：配方可得f（x）=x2+2x-2=（x+1）2-3，
由二次函数知识可知，函数在（-3，-1）单调递减，在（-1，1）单调递增，
∴当x=-1时，函数取最小值-3，当x=1时，函数取最大值1，
∴f（x）的值域为：[-3，1]
故答案为：[-3，1]
由二次函数知识可知，函数在（-3，-1）单调递减，在（-1，1）单调递增，
∴当x=-1时，函数取最小值-3，当x=1时，函数取最大值1，
∴f（x）的值域为：[-3，1]
故答案为：[-3，1]
点评：本题考查二次函数区间的值域，属基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
| 5 | a-2 |
A、a -
| ||
B、a
| ||
C、a
| ||
D、-a
|
在各项均为正数的等比数列{an}中，若a5a6=27，则log3a1+log3a2+…+log3a10=（ ）
| A、12 |
| B、10 |
| C、15 |
| D、27log35 |
已知cos（
+a）=
，-
＜a＜0，则sin2α的值是（ ）
| 5π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
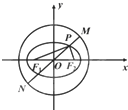如图，已知椭圆C：