题目内容
4.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点为F(-1,0),O为坐标原点,点$G({1,\frac{{\sqrt{2}}}{2}})$在椭圆上,过点F的直线l交椭圆于不同的两点 A、B.(1)求椭圆C的方程;
(2)求弦AB的中点M的轨迹方程.
分析 (1)利用椭圆的焦点坐标,椭圆经过的点,列出a,b方程组,求解可得椭圆方程;
(2)设M(x,y),A(x1,y1),B(x2,y2),利用中点坐标公式以及平方差公式,化简可得M的轨迹方程.
解答 解:(1)由题意有a2-b2=1,且$\frac{1^2}{a^2}+\frac{{{{(\frac{{\sqrt{2}}}{2})}^2}}}{b^2}=1$,
解得a2=2,b2=1,
∴椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$.…(4分)
(2)设M(x,y),A(x1,y1),B(x2,y2),则$x=\frac{{{x_1}+{x_2}}}{2}$,$y=\frac{{{y_1}+{y_2}}}{2}$
当x1=x2时,M点的坐标为(-1,0).
当x1≠x2时,
∵$\frac{{{x_1}^2}}{2}+{y_1}^2=1$,$\frac{{{x_2}^2}}{2}+{y_2}^2=1$,
两式相减得$\frac{{({x_1}+{x_2})(x{\;}_1-{x_2})}}{2}=-({y_1}+{y_2})({y_1}-{y_2})$,
∴$\frac{2x}{2•2y}=-\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$.
又AB过F点,于是AB的斜率为$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{y-0}{x+1}$,
∴$\frac{x}{2y}$=$-\frac{y}{x+1}$,
整理得x2+2y2+x=0.
∵(-1,0)也满足上式,
∴M的轨迹方程为x2+2y2+x=0.…(12分)
点评 本题考查椭圆的简单性质,椭圆方程的求法,轨迹方程的求法,考查转化思想以及计算能力.

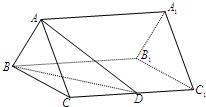 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°. 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.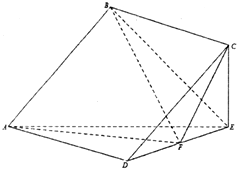 在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.
在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.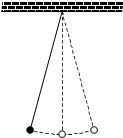 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.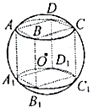 如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )
如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )