题目内容
8.已知函数$f(x)=sinx+sin(x+\frac{π}{2})$.(1)求f(x)的最小正周期、最大值及取得最大值时x的取值集合;
(2)求f(x)的递减区间.
分析 (1)由条件利用诱导公式、两角和的正弦公式化简函数的解析式,再利用正弦函数的周期性和最大值得出结论.
(2)根据正弦函数的单调性求得f(x)的递减区间.
解答 解:(1)对于函数$f(x)=sinx+sin(x+\frac{π}{2})$=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
它的最小正周期为$\frac{2π}{1}$=2π;
它的最大值为$\sqrt{2}$,此时,x+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,即x=2kπ+$\frac{π}{4}$,k∈Z,
故函数取得最大值时x的取值集合为{x|x=2kπ+$\frac{π}{4}$,k∈Z }.
(2)令 2kπ+$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得 kπ+$\frac{π}{8}$≤x≤2kπ+$\frac{5π}{8}$,
故函数的减区间为[kπ+$\frac{π}{8}$,2kπ+$\frac{5π}{8}$],k∈Z.
点评 本题主要考查诱导公式、两角和的正弦公式,正弦函数的周期性和最大值,正弦函数的单调性,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.已知等差数列{an}中,a1=4,a2=6,则S4=( )
| A. | 18 | B. | 21 | C. | 28 | D. | 40 |
20.判断下列各对直线的位置关系,如果相交,求出交点坐标:
(1)l1:2x-y+7=0,l2:x+y=1;
(2)${l_1}:x-3y-10=0,\;\;{l_2}:y=\frac{x+5}{3}$.
(1)l1:2x-y+7=0,l2:x+y=1;
(2)${l_1}:x-3y-10=0,\;\;{l_2}:y=\frac{x+5}{3}$.
17.下列函数中,既是奇函数又存在零点的函数是( )
| A. | y=sinx | B. | y=cosx | C. | y=lnx | D. | y=x3+1 |
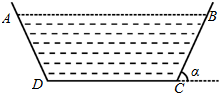 2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?
2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?