题目内容
16.若点 P(1,2),A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的不同的三个点,直线AP,BP的斜率分别是k1,k2,若k1+k2=0.(1)求抛物线的方程;
(2)求y1+y2的值及直线AB的斜率k.
分析 (1)把P的坐标代入抛物线方程求得p,则抛物线方程可求;
(2)分别设出直线PA、PB的方程,和抛物线方程联立,利用根与系数的关系求出A,B的纵坐标,作和得答案;再由斜率公式求出AB的斜率,整体代入y1+y2的值求得直线AB的斜率k.
解答 解:(1)∵P(1,2)在抛物线y2=2px(p>0)上,
∴22=2p,即p=2,
∴抛物线方程为y2=4x;
(2)由题意设PA所在直线方程为y-2=k(x-1),
联立$\left\{\begin{array}{l}{y=k(x-1)+2}\\{{y}^{2}=4x}\end{array}\right.$,得ky2-4y-4k+8=0.
∴${y}_{1}+2=\frac{4}{k}$,得${y}_{1}=\frac{4}{k}-2$.
设PB所在直线方程为y-2=-k(x-1),
联立$\left\{\begin{array}{l}{y=-k(x-1)+2}\\{{y}^{2}=4x}\end{array}\right.$,得ky2+4y-4k-8=0.
∴${y}_{2}+2=-\frac{4}{k}$,得${y}_{2}=-\frac{4}{k}-2$.
∴y1+y2=-4;
${k}_{AB}=\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=\frac{{y}_{1}-{y}_{2}}{\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{4}}=\frac{4}{{y}_{1}+{y}_{2}}=\frac{4}{-4}=-1$.
点评 本题考查抛物线的方程,考查了直线与抛物线的关系,体现了“设而不求”的解题思想方法和整体运算思想方法,是中档题.

练习册系列答案
相关题目
1.已知一个算法,其流程图如图所示,则输出结果是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
5.已知a、b、c表示不同的直线,α、β、γ表示不同的平面,则下列判断正确的是( )
| A. | 若a⊥c,b⊥c,则a∥b | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若α⊥a,β⊥a,则α∥β | D. | 若a⊥α,b⊥a,则b∥α |
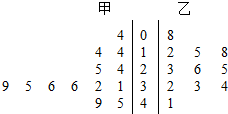 现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.
现今社会对食品安全的高度重视,各级政府加强了对食品安全的检查力度.某市工商质检局抽派甲、乙两个食品质量检查组到管辖区域内的商店进行食品质量检查.如图表示甲、乙两个检查组每天检查到的食品品种数的茎叶图,则甲、乙两个检查组每天检查到的食品种数的中位数的和是58.