题目内容
| 2cos10° |
| cos20° |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：将所求关系式中的“切”化“弦”，再通分，利用辅助角公式与诱导公式即可求得答案．
解答：
解：∵
-tan20°
=
-
=
-
=
-
=
-
=
．
故选：C．
| 2cos10° |
| cos20° |
=
| 2cos10° |
| cos20° |
| sin20° |
| cos20° |
=
| 2cos(30°-20°) |
| cos20° |
| sin20° |
| cos20° |
=
| 2(cos30°cos20°+sin30°sin20°) |
| cos20° |
| sin20° |
| cos20° |
=
| ||
| cos20° |
| sin20° |
| cos20° |
=
| 3 |
故选：C．
点评：本题考查三角函数的化简求值，“切”化“弦”是关键，cos10°=cos（30°-20°）的应用是难点，考查分析与运算能力，属于中档题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
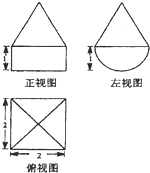某几何体的三视图如图所示，其中正视图和左视图的上半部分均为边长为2的等边三角形，则该几何体的体积为（ ）A、π+
| ||||
B、2π+
| ||||
C、π+
| ||||
D、2π+
|
曲线
+
=1与曲线
+
=1（k＜3）的（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-k |
| y2 |
| 3-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
下列几何图形的主视图不能是三角形的是（ ）
| A、三棱柱 | B、圆台 |
| C、四棱锥 | D、圆锥 |