题目内容
已知抛物线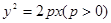
的焦点为
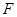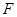，关于原点的对称点为
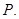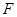过作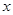
轴的垂线交抛物线于
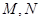两点．有下列四个命题：①
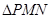必为直角三角形；②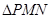不一定为直角三角形；③直线
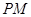必与抛物线相切；④直线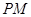不一定与抛物线相切．其中正确的命题是
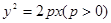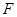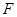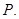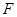的焦点为，关于原点的对称点为过作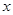轴的垂线交抛物线于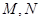两点．有下列四个命题：①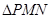必为直角三角形；②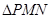不一定为直角三角形；③直线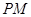必与抛物线相切；④直线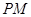不一定与抛物线相切．其中正确的命题是| A．①③ | B．①④ | C．②③ | D．②④ |
A
由已知可得：
，
，所以
，即
必为直角三角形抛物线
的图像在x轴上面的部分可用函数
，
，抛物线在M点处的切线斜率
，而
，直线
必与抛物线相切故选择A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
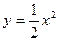与直线l：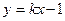
没有公共点，设点P为直线l上的动点，过P作抛物线C的两条切线，A，B为切点．
．
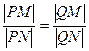的焦点与椭圆
的右焦点重合，则p的值为 （ ）
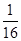
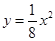的焦点坐标是 ．
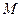到定点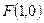
的距离与到定直线
：
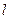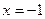的距离相等，点C在直线
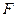，且法向量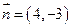
的直线与（1）中的轨迹相交于
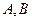两点且点
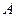在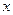
轴的上方。判断
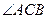能否为钝角并说明理由。进一步研究
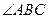为钝角时点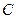
纵坐标的取值范围。
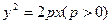上有一点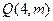
到焦点的距离为5，
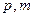的值；
线
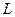交抛物线于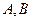
两点，求线段
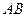的长。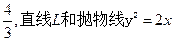
相交于A，B两点，设线段AB
的中点为M，求：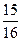
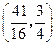
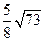
，则抛物线的焦点坐标为________
与抛物线C：
相交于A.B两点，F为C的焦点，若
，
则
（ ）
B. 
C. 
D. 