题目内容
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则p的值为 ( )
的右焦点重合,则p的值为 ( )
 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则p的值为 ( )
的右焦点重合,则p的值为 ( )A.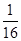 | B. | C. | D.4 |
A
分析:根据椭圆方程算出椭圆右焦点是(2,0),由抛物线方程得抛物线的焦点为(
 ,0),因此建立关于p的方程,解之即可得到实数p的值.
,0),因此建立关于p的方程,解之即可得到实数p的值.解:∵抛物线方程为y2=
 x,
x,∴抛物线的焦点为F(
 ,0)
,0)∵椭圆的方程为

∴c=
 =2,得到椭圆右焦点是(2,0),
=2,得到椭圆右焦点是(2,0),结合椭圆右焦点与抛物线的焦点重合,得
 =2,解之得p=
=2,解之得p=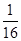
故选:A

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
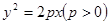 的准线与圆
的准线与圆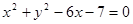 相切,则
相切,则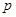 的值为
的值为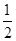
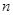 ,设抛物线
,设抛物线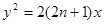 ,过
,过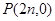 任作直线
任作直线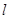 交抛物线于
交抛物线于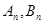 两点,则数列
两点,则数列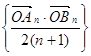 的前
的前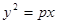 的焦点与椭圆
的焦点与椭圆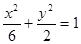 的右焦点重合,则p的值为
的右焦点重合,则p的值为

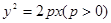 的焦点为
的焦点为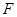 ,
,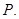 过
过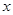 轴的垂线交抛物线于
轴的垂线交抛物线于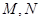 两点.有下列四个命题:①
两点.有下列四个命题:①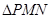 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线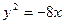 的准线与双曲线
的准线与双曲线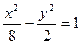 的两条渐近线所围成的三角形的面积为
的两条渐近线所围成的三角形的面积为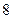 B.
B.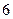 C.
C.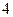 D. 2
D. 2 的焦点,与抛物线交于两点A、B,将直线AB按向量
的焦点,与抛物线交于两点A、B,将直线AB按向量 平移得直线
平移得直线 ,N为
,N为
 的最小值。
的最小值。 的焦点到准线的距离是( )
的焦点到准线的距离是( )



 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 = .
= .