题目内容
11.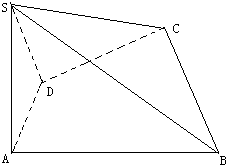 如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,
如图四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,(1)若SB上存在一点E,使得CE∥平面SAD,求$\frac{SE}{SB}$的值;
(2)求此四棱锥体积的最大值;
(3)当体积最大时,求二面角A-SC-B大小的余弦值.
分析 (1)过C作AD的平行线CF,交AB于F,过F作SA的平行线FE,交SB于E,则点E就是所求的点,由此能求出结果.
(2)当SA⊥平面ABCD时,此四棱锥体积最大,由此能求出此四棱锥体积的最大值.
(3)当体积最大时,SA⊥平面ABCD,连结AC,取AC的中点O,过O作OK⊥SC,垂足为K,连结BK,由三垂线定理得BK⊥SC,∠BKO是二面角A-SC-B的平面角,由此能求出当体积最大时,二面角A-SC-B的余弦值.
解答 解:(1)过C作AD的平行线CF,交AB于F,
过F作SA的平行线FE,交SB于E,
∵AD∥CF,SA∥FE,AD∩AS=A,CF∩EF=F,
AD,AS?平面ADS,CF,EF?平面CEF,
∴平面ADS∥平面CEF,
∵CE?平面CEF,∴CE∥平面SAD,
∵四棱锥S-ABCD,底面四边形ABCD满足条件∠DAB=90°,
∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,侧面SAD垂直于底面ABCD,SA=2,
∴AF=AD=2,CF=4,BF=5-2=3,
∴$\frac{SE}{SB}$=$\frac{AF}{AB}$=$\frac{2}{5}$.
(2)当SA⊥平面ABCD时,此四棱锥体积最大,
∵SA=2,AF=AD=2,CF=4,BF=5-2=3,∠DAB=90°,
∴S四边形ABCD=S梯形AFCD+S△BCF
=$\frac{1}{2}(2+4)×2+\frac{1}{2}×4×3$=12,
∴此四棱锥体积的最大值V=$\frac{1}{3}×{S}_{四边形ABCD}×SA$=$\frac{1}{3}×12×2$=8.
(3)当体积最大时,SA⊥平面ABCD,连结AC,取AC的中点O,
∵BF=3,CF=4,BF⊥CF,∴BC=5,
∴BA=BC=5,∴BO⊥AC,
∵SA⊥平面ABCD,BO?平面ABCD,∴BO⊥SA,
∵SA∩AC=A,∴BO⊥平面SAC,
过O作OK⊥SC,垂足为K,连结BK,
则由三垂线定理得BK⊥SC,
∴∠BKO是二面角A-SC-B的平面角,
AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=2$\sqrt{5}$,SC=$\sqrt{A{C}^{2}+S{A}^{2}}$=2$\sqrt{6}$,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=2$\sqrt{5}$,
∵S△SOC=S△SAC-S△SAO,
∴$\frac{1}{2}×SC×OK=\frac{1}{2}×SA×AC-\frac{1}{2}×SA×AO$,
∴$\sqrt{6}$×OK=$\frac{1}{2}×2×2\sqrt{5}-\frac{1}{2}×2×\sqrt{5}$=$\sqrt{5}$,∴OK=$\frac{\sqrt{5}}{\sqrt{6}}$,
∴BK=$\sqrt{O{K}^{2}+O{B}^{2}}$=$\frac{5\sqrt{5}}{\sqrt{6}}$,
∴cos∠BKO=$\frac{OK}{BK}$=$\frac{1}{5}$.
∴当体积最大时,二面角A-SC-B的余弦值为$\frac{1}{5}$.
点评 本题考查满足条件的点的位置的确定及求法,考查四棱锥的体积的最大值的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 钝角 | B. | 直角 | C. | 锐角 | D. | 60° |
| A. | ab=0 | B. | a+b=0 | C. | a2+b2=0 | D. | a=b |
| A. | {x|{$\frac{3}{2}$<x<2} | B. | {x|${\frac{1}{2}$<x<2} | C. | {x|x<1} | D. | {x|-1<x<$\frac{3}{2}}\right.$} |
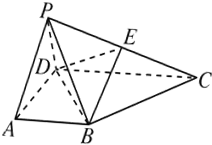 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.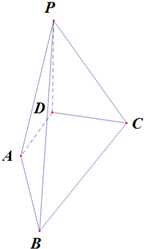 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.