题目内容

1．在△ABC中，若sin2A+sin2B=2sin2C，则角C为（　　）
A．钝角B．直角C．锐角D．60°

分析 已知等式利用正弦定理化简，再利用余弦定理判断出cosC的正负，即可确定出C．

解答 解：在△ABC中，sin2A+sin2B=2sin2C，
利用正弦定理化简得：a2+b2=2c2，
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{c}^{2}}{2ab}$＞0，即C为锐角，
故选：C．

点评 此题考查了余弦定理，以及正弦定理，熟练掌握正弦、余弦定理是解本题的关键．

练习册系列答案
相关题目
9．已知f（x）=ex，g（x）=lnx．
（1）若f（$\frac{1}{e}$x）-ax≥0恒成立（a≥0），求a的取值范围；
（2）求证：f（$\frac{1}{e}$x）-g（x-e）＞1．

已知函数的定义域为，值域为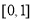，那么满足条件的整数对共有（ ）

A．6个 B．7个

C.8个 D．9个
9．设函数f（x）=sin（2x+$\frac{π}{2}$）-4cos（π-x）sin（x-$\frac{π}{6}$）
（1）求f（0）的值；
（2）求f（x）的单调递增区间．
16．已知△ABC的三个顶点的坐标为A（-1，0）、B（4，0）、C（0，c）．
（1）若$\overrightarrow{AC}$⊥$\overrightarrow{BC}$，求c的值；
（2）当c满足（1）问题的结论时，求△ABC的重心坐标G（x，y）．
6．已知焦点在x轴上的椭圆C为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{{b}^{2}}$=1，F1、F2分别是椭圆C的左、右焦点，离心率e=$\frac{\sqrt{2}}{2}$．
（1）求椭圆C的方程；
（2）设点Q的坐标为（1，0），椭圆上是否存在一点P，使得直线PF1，PF2都与以Q为圆心的一个圆相切？若存在，求出P点坐标及圆的方程；若不存在，请说明理由．
13．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{6}}}{3}$，上顶点为（0，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过原点O作两条互相垂直的射线，与椭圆C交于A，B两点，求证：点O到直线AB的距离为定值．
10．随机变量ξ的分布列为：
ξ0123
Px0.20.30.4
随机变量ξ的方差D（ξ）1．
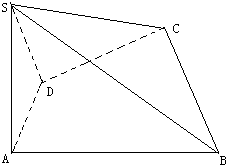11．如图四棱锥S-ABCD，底面四边形ABCD满足条件∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，侧面SAD垂直于底面ABCD，SA=2，
（1）若SB上存在一点E，使得CE∥平面SAD，求$\frac{SE}{SB}$的值；
（2）求此四棱锥体积的最大值；
（3）当体积最大时，求二面角A-SC-B大小的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网