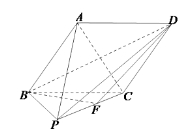
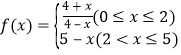题目内容
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

【答案】(1)函数![]() ,定义域是
,定义域是![]() (2)
(2)![]()
【解析】试题分析:
(1)利用题意结合余弦定理可得函数的解析式![]() ,其定义域是
,其定义域是![]() .
.
(2)结合(1)的结论求得利润函数,由均值不等式的结论即可求得当![]() km时,公司建中转站围墙和两条道路最低总造价
km时,公司建中转站围墙和两条道路最低总造价![]() 为490万元.
为490万元.
试题解析:
(1)在![]() 中,
中,![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,
由余弦定理,得![]() ,
,
即 ![]() ,
,
所以 ![]() .
.
由![]() , 得
, 得![]() . 又因为
. 又因为![]() ,所以
,所以![]() .
.
所以函数![]() 的定义域是
的定义域是![]() .
.
(2)![]()
![]() .
.
因为![]() (
(![]()
![]()
即 ![]() .
.
令![]() 则
则![]() . 于是
. 于是![]() ,
,
由基本不等式得![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
答:当![]() km时,公司建中转站围墙和两条道路最低总造价
km时,公司建中转站围墙和两条道路最低总造价![]() 为490万元.
为490万元.

练习册系列答案
相关题目